CL_to_CT过程记录
✌探测器旋转变换
X轴的方向向量
$$ \vec{a} = \left ( SDD,\left ( R_1-R_2 \right )cos\alpha ,\left ( R_1- R_2 \right ) sin\alpha \right ) $$ $$ 单位向量 \vec{x} =\hat{\vec{a}} = \left ( \frac{SDD }{\sqrt{SDD^2+(R_1+R_2)^2}} ,\frac{\left ( R_1+R_2 \right )cos\alpha}{\sqrt{SDD^2+(R_1+R_2)^2}} ,\frac{\left ( R_1+R_2 \right )sin\alpha}{\sqrt{SDD^2+(R_1+R_2)^2}} \right ) $$Y轴方向向量
$$ \vec{b} = \left ( R_1+R_2,-SDDcos\alpha ,-SDDsin\alpha \right ) $$单位向量为:
$$ \vec{y} =\hat{\vec{b}} = \left ( \frac{R_1+R_2}{\sqrt{SDD^2+(R_1+R_2)^2}} ,\frac{-SDDcos\alpha}{\sqrt{SDD^2+(R_1+R_2)^2}} ,\frac{-SDDsin\alpha}{\sqrt{SDD^2+(R_1+R_2)^2}} \right ) $$Z轴方向向量
$$
\vec{c} =\left ( 0,-sin\alpha ,cos\alpha \right )
$$
$$
\vec{z} =\hat{\vec{c}} =\left ( 0,-sin\alpha ,cos\alpha \right )
$$
$$
\alpha = \tan^{-1} \left ( \frac{-n_z}{\sqrt{n_x^2+n_y^2} } \right ) \beta = \tan^{-1} \left ( \frac{n_y}{n_z} \right ) \gamma = \tan^{-1} \left ( \frac{o_z}{a_z} \right ) ,
$$

我们需要从给定矩阵中计算出 (\alpha)、(\beta) 和 (\gamma) 的值。给定的矩阵是:
$$ \begin{bmatrix} n_x & o_x & a_x \\n_y & o_y & a_y \\n_z & o_z & a_z \end{bmatrix}= \begin{bmatrix} \frac{SDD }{\sqrt{SDD^2+(R_1+R_2)^2}}& \frac{R_1+R_2}{\sqrt{SDD^2+(R_1+R_2)^2}} &0 \\ \frac{\left ( R_1+R_2 \right )cos\alpha}{\sqrt{SDD^2+(R_1+R_2)^2}} & \frac{-SDDcos\alpha}{\sqrt{SDD^2+(R_1+R_2)^2}} & -sin\alpha \\ \frac{\left ( R_1+R_2 \right )sin\alpha}{\sqrt{SDD^2+(R_1+R_2)^2}}& \frac{-SDDsin\alpha}{\sqrt{SDD^2+(R_1+R_2)^2}} &cos\alpha \end{bmatrix} $$根据给定的公式:
$$
1.
\alpha = \tan^{-1} \left( \frac{-n_z}{\sqrt{n_x^2 + n_y^2}} \right)\
2. \beta = \tan^{-1} \left( \frac{n_y}{n_x} \right)\
3. \gamma = \tan^{-1} \left( \frac{o_z}{a_z} \right)
$$
$$ 1. \beta = \tan2 \left( -n_z,\sqrt{n_x^2 + n_y^2} \right)\\2. \delta = \tan2 \left(\frac{n_y}{cos\beta },\frac{n_x}{cos\beta} \right)\\3. \gamma = \tan2 \left( \frac{o_z}{cos\beta },\frac{a_z}{cos\beta} \right) $$或者
最终结果
图片结果有点问题,以公式为准;
$$
\beta =\tan^{-1} \left ( \frac{-\left ( R_1+R_2 \right )sin\alpha}{\sqrt{SDD^2+(R_1+R_2)^2cos\alpha^2}} \right ) \
$$
$$
\delta = \tan^{-1} \left ( \frac{\left ( R_1+R_2 \right )cos\alpha }{SDD} \right ) \
$$
$$
\gamma = \tan^{-1} \left (-\frac{SDDsin\alpha}{cos\alpha \sqrt{SDD^2+(R_1+R_2)^2}} \right )
$$

其中 绕Z轴转$\delta $,绕y轴转$\beta$,绕X轴转γ
$$ \begin{bmatrix} n_x & o_x & a_x \\n_y & o_y & a_y \\n_z & o_z & a_z \end{bmatrix}= \begin{bmatrix} \frac{SDD }{\sqrt{SDD^2+(R_1-R_2)^2}}& \frac{R_1-R_2}{\sqrt{SDD^2+(R_1-R_2)^2}} &0 \\ \frac{\left ( R_1-R_2 \right )cos\alpha}{\sqrt{SDD^2+(R_1-R_2)^2}} & \frac{-SDDcos\alpha}{\sqrt{SDD^2+(R_1-R_2)^2}} & -sin\alpha \\ \frac{\left ( R_1-R_2 \right )sin\alpha}{\sqrt{SDD^2+(R_1-R_2)^2}}& \frac{-SDDsin\alpha}{\sqrt{SDD^2+(R_1-R_2)^2}} &cos\alpha \end{bmatrix}这是位姿矩阵,用公式1. \beta = \tan2 \left( -n_z,\sqrt{n_x^2 + n_y^2} \right)\\2. \delta = \tan2 \left(\frac{n_y}{cos\beta },\frac{n_x}{cos\beta} \right)\\3. \gamma = \tan2 \left( \frac{o_z}{cos\beta },\frac{a_z}{cos\beta} \right),求出\alpha,\beta, \gamma $$ $$ \begin{bmatrix} n_x & o_x & a_x \\n_y & o_y & a_y \\n_z & o_z & a_z \end{bmatrix}= \begin{bmatrix} \frac{SDD }{\sqrt{SDD^2+(R_1+R_2)^2}}& \frac{R_1+R_2}{\sqrt{SDD^2+(R_1+R_2)^2}} &0 \\ \frac{\left ( R_1+R_2 \right )cos\alpha}{\sqrt{SDD^2+(R_1+R_2)^2}} & \frac{-SDDcos\alpha}{\sqrt{SDD^2+(R_1+R_2)^2}} & -sin\alpha \\ \frac{\left ( R_1+R_2 \right )sin\alpha}{\sqrt{SDD^2+(R_1+R_2)^2}}& \frac{-SDDsin\alpha}{\sqrt{SDD^2+(R_1+R_2)^2}} &cos\alpha \end{bmatrix}这是位姿矩阵,用公式1. \delta = \tan^{-1} \left( \frac{-n_z}{\sqrt{n_x^2 + n_y^2}} \right)\\ 2. \beta = \tan^{-1} \left( \frac{n_y}{n_x} \right)\\ 3. \gamma = \tan^{-1} \left( \frac{o_z}{a_z} \right),求出\delta,\beta, \gamma $$问题
✌投影数据转换过程
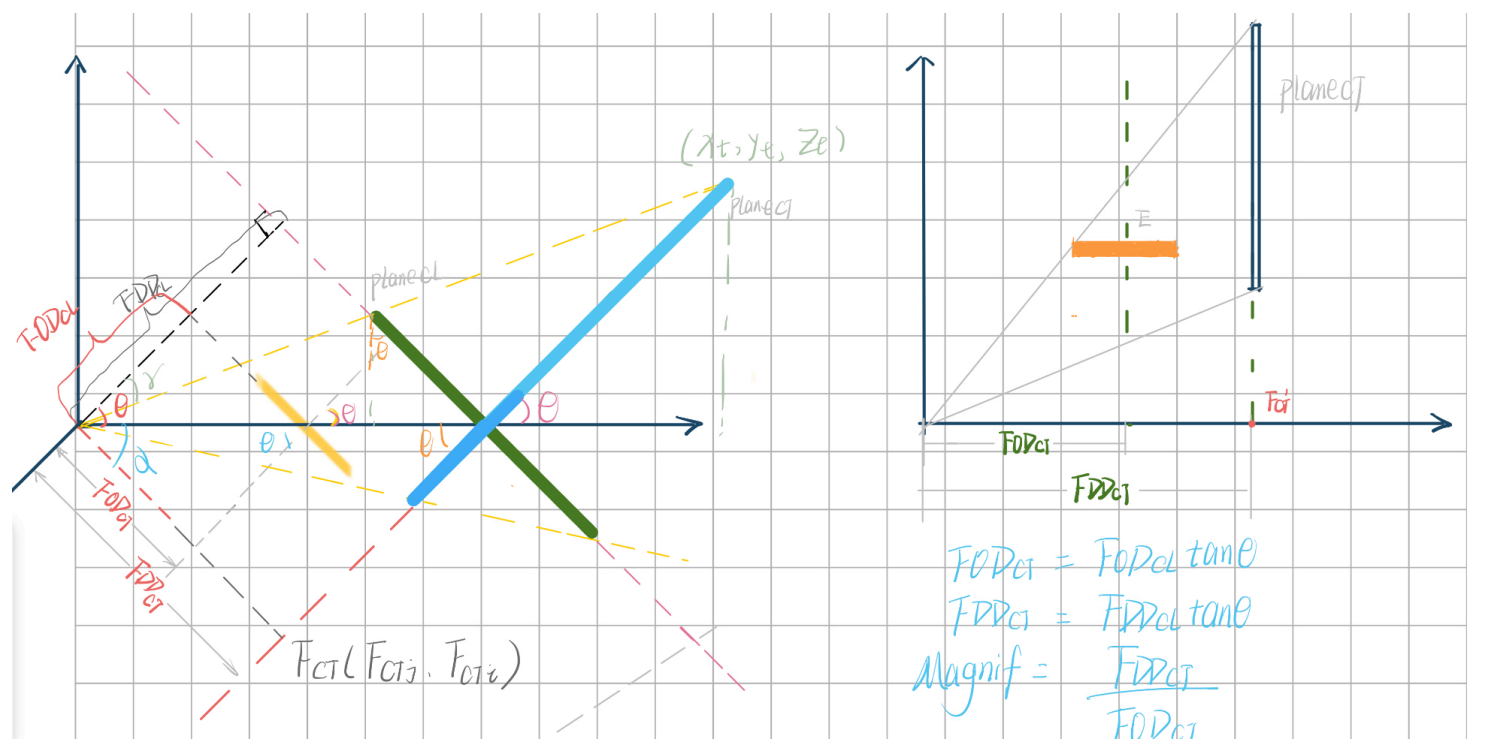
令CL探测器的的像素尺寸为$P_{size}$,则CL探测器中的像素坐标$(j,i)$的空间坐标为
$$
\begin{Bmatrix}x_w = (i - F_{cli} )P_{size} \y_w = (\frac{FDD{cl}}{cos\theta} + (j - F_{clj})sin\theta P_{size} \z_w = (F_{clj} - j)cos\theta P_{size}\end{Bmatrix},j\in [1,height],i\in[1,width]
$$
对于CT投影面,令其单位向量$\vec{n} = (0,-sin\theta, cos\theta )$,平面中空间内一点的空间坐标为$(0,\frac{FDD_{cl}}{cos\theta},0)$,则CT投影平面方程为
$$
ysin\theta -zcos\theta -FDD_{cl}tan\theta =0
$$
投影面$A’B’C’D’$中各个像素点的空间坐标$({x_w}’ ,{}y_w’,{z_w’)}$的计算公式为:
$$
\begin{bmatrix}x_w’ \y_w’ \z_w’\end{bmatrix}=\frac{FDD_{cl}tan\theta}{y_wsin\theta-z_wcos\theta}\begin{bmatrix}x_w \y_w \z_w\end{bmatrix}
$$
根据投影矩阵的行列坐标 A (1,1)、B (1,width)、C (height, width ) 、D (height ,1) 可知,结合式(4.1)和式(4.3)即可得到 A’、B’、C’、D’的空间坐标。
$PQRS$ 投影面中像素点的x方向空间坐标范围$[x_P,x_Q]$ ,等价于$[min(x_{A’},x_{D’}),max(x_{B’},x_{C’})]]$; y 方向空间坐标范围是$[y_p,y_s]$,等价于$[y_{A}’,y_{D}’]$。$PQRS $ 投影面在i轴的像素尺寸为$|(x_Q-x_P)/P_{size}|$, $j$轴的像素尺寸为$|y_p-y_s|/(P_{size}cos\theta)$.
根据空间坐标范围$[x_P,x_Q] $、$[y_P,y_S]$和行列方向的像素尺寸可以生成 $ PQRS$ 平面的等效 CT 投影矩阵。令$ PORS$ 投影面中的空间坐标为$(x_t,y_t,z_t)$,在计算$PQRS$投影面中的投影值时,首先找到待计算的像素点对应的$(x_t,y_t)$,将$(x_t,y_t)$代入式(4.2)即可得到$(x_t,y_t,z_t)$。
根据$Panel_{CT} $到 $Panel_{CL} $ 几何映射关系可知,$\gamma = \theta - \arctan (z_t/y_t)$,投影面 $ PQRS$ 中$(x_t,y_t,z_t)$处的投影值对应投影面 $ABCD$ 中$\left ( FDD{cl}/cos\gamma\cdot \frac{x_t}{\sqrt[]{y_t^2+z_t^2} },FDD{cl}/cos\gamma\cdot \frac{y_t}{\sqrt[]{y_t^2+z_t^2} } ,FDD{cl}/cos\gamma\cdot \frac{z_t}{\sqrt[]{y_t^2+z_t^2} }\right ) $处的投影值。在实际计算时,可以通过双线性插值来获取投影值。通过以上步骤即可得到转换后的等效 CT 投影数据。
Latex公式
\begin{Bmatrix}x_w = (i - F_{cli} )P_{size} |
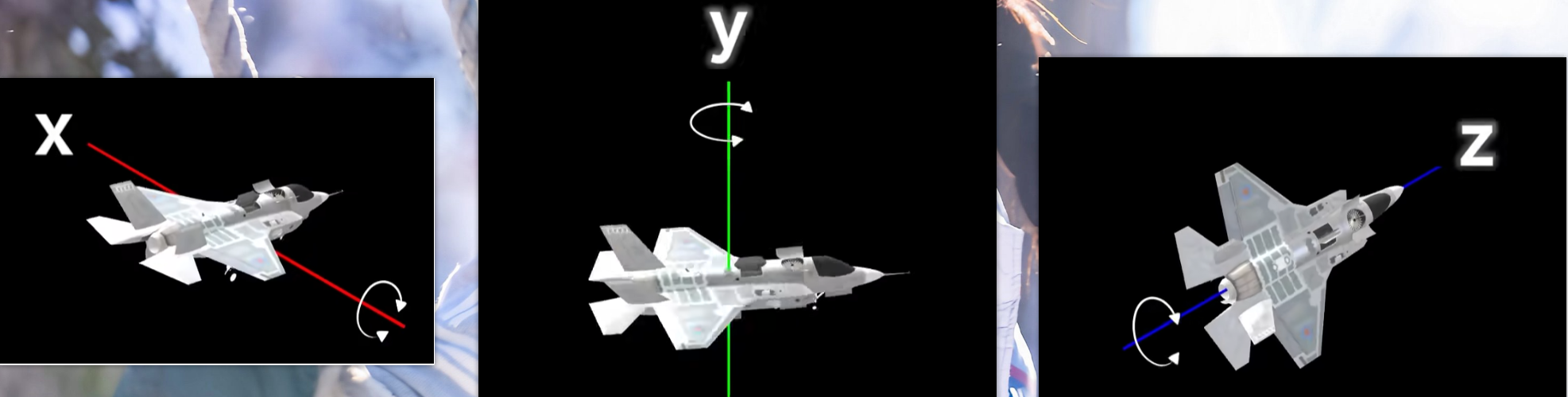
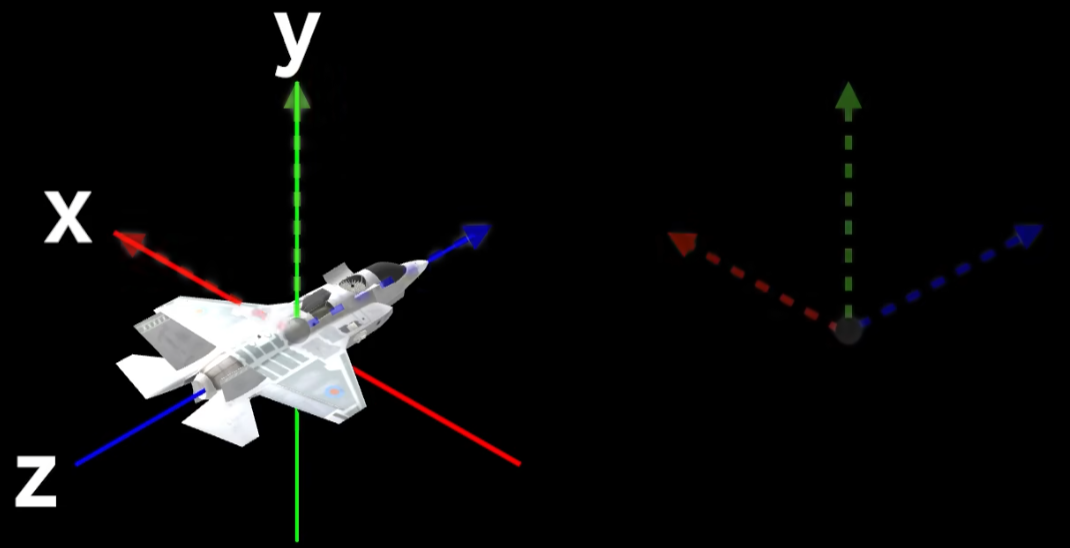
欧拉角
俯仰——绕X轴进行旋转
转向——绕Y轴进行旋转
翻滚——绕Z轴进行旋转