🤔什么是神经网络

  • 神经元中装着的数字代表对应的像素的灰度值，0表示纯黑像素，1表示纯白像素。神经元中装着的数称为“激活值”。
  • 神经网络处理信息的核心机制是一层的激活值是通过怎样的运算算出下一层的激活值
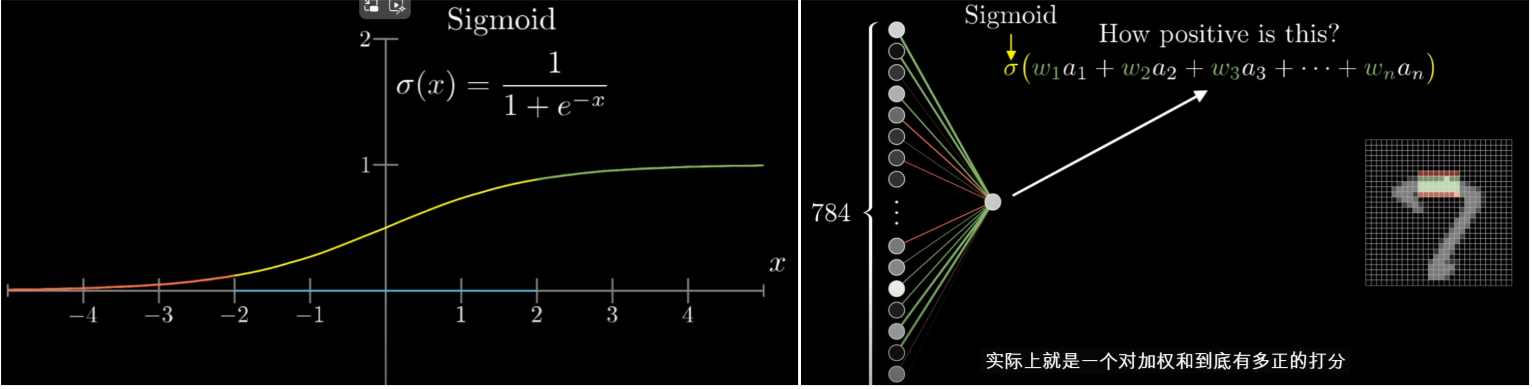
  • 所谓神经元的激活值实际上就是对加权和到底有多正的打分

image-20240516164546935

image-20240516170232107

image-20240516171707220

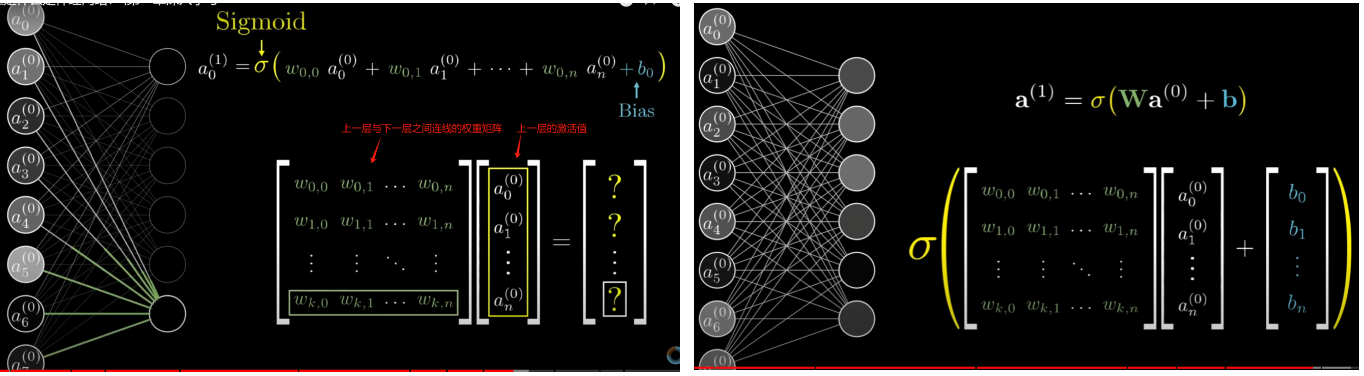
image-20240516185215679
$$
a^{(1)} = \sigma(Wa^{(0)} + b)
$$

  • 权重像是连接的强度，而偏差是该神经元是否倾向于活跃或不活跃。

💆‍♀️梯度下降，神经网络如何学习|深度学习

需要考虑可以使用的所有数以万计的训练示例的平均成本，这个成本是衡量网络有多糟糕的标准

image-20240516193200669

image-20240516193357520

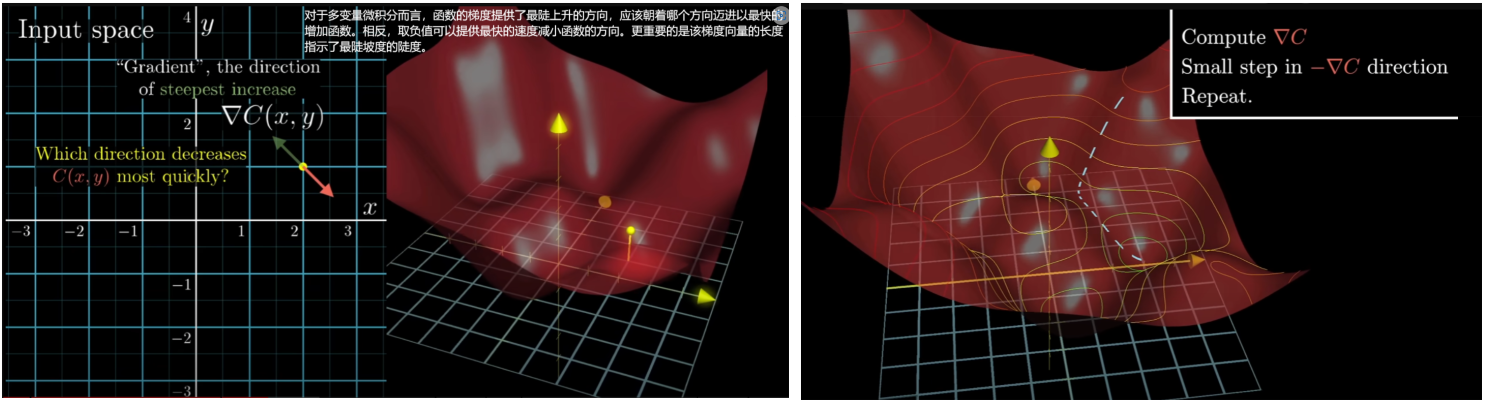
  • 对于多变量微积分而言，函数的梯度提供了最陡上升的方向，应该朝着哪个方向迈进以最快的增加函数。相反，取负值可以提供最快的速度减小函数的方向。更重要的是该梯度向量的长度指示了最陡坡度的陡度。

  • 最小化函数的算法就是计算这个梯度反向，然后向下走一小步，然后不断重复这个过程

image-20240516202129474

  • 有效计算梯度的算法被称为反向传播，它实际上是神经网络的核心
  • 损失函数是指用来衡量模型的预测值和真实值之间的不一致程度的函数

image-20240516211400639

梯度就是函数对它的各个自变量求偏导后，由偏导数组成的一个向量。

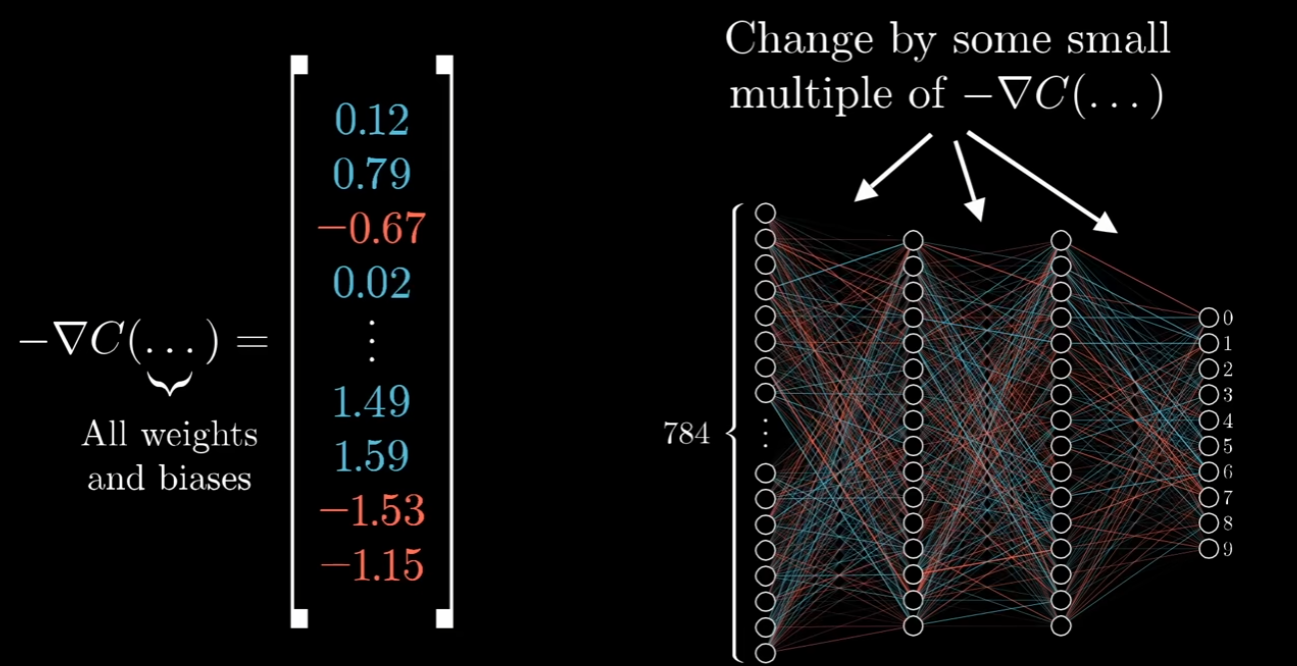
负梯度的每个分量告诉我们两件事，符号告诉我们输入向量的相应分量是否应该向上或者向下位移、他编码了每个权重和偏差的相对重要性，也就是这些变化中哪一个将为您带来巨大收益、如何改变所有连线上的权重偏置，使得损失下降的最快。

  • 那么这个梯度向量求出来有什么意义呢？他的意义从几何意义上讲，就是函数变化增加最快的地方。具体来说，对于函数f(x,y),在点$ (x_0,y_0)$，沿着梯度向量的方向就是$(∂f/∂x_0 ,∂f/∂y_0 )^T $,是f(x,y)增加最快的地方。或者说，沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方向，也就是$-(∂f/∂x_0 ,∂f/∂y_0 )^T $ 的方向，梯度减少最快，也就是更加容易找到函数的最小值。
  • 所以所谓的“梯度”就是求偏导，“梯度下降”就是沿着“导数值”减小的方向（负梯度方向），这样就可使得损失函数快速减小，误差就减小。在机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值.
  • 所谓的学习就是指找到特定的权重偏置，从而使损失函数最小化

小白零基础学习：详解梯度下降算法：完整原理+公式推导+视频讲解_标准梯度下降算法 损函数-CSDN博客

image-20240516213607795

如果想了解更多，我强烈建议您阅读这本由Michael Nielse写的书：Neural networks and deep learning

这本书讲解了视频中一些实例的代码，你可以在这里找到它：mnielsen/neural-networks-and-deep-learning: Code samples for my book “Neural Networks and Deep Learning” (github.com)

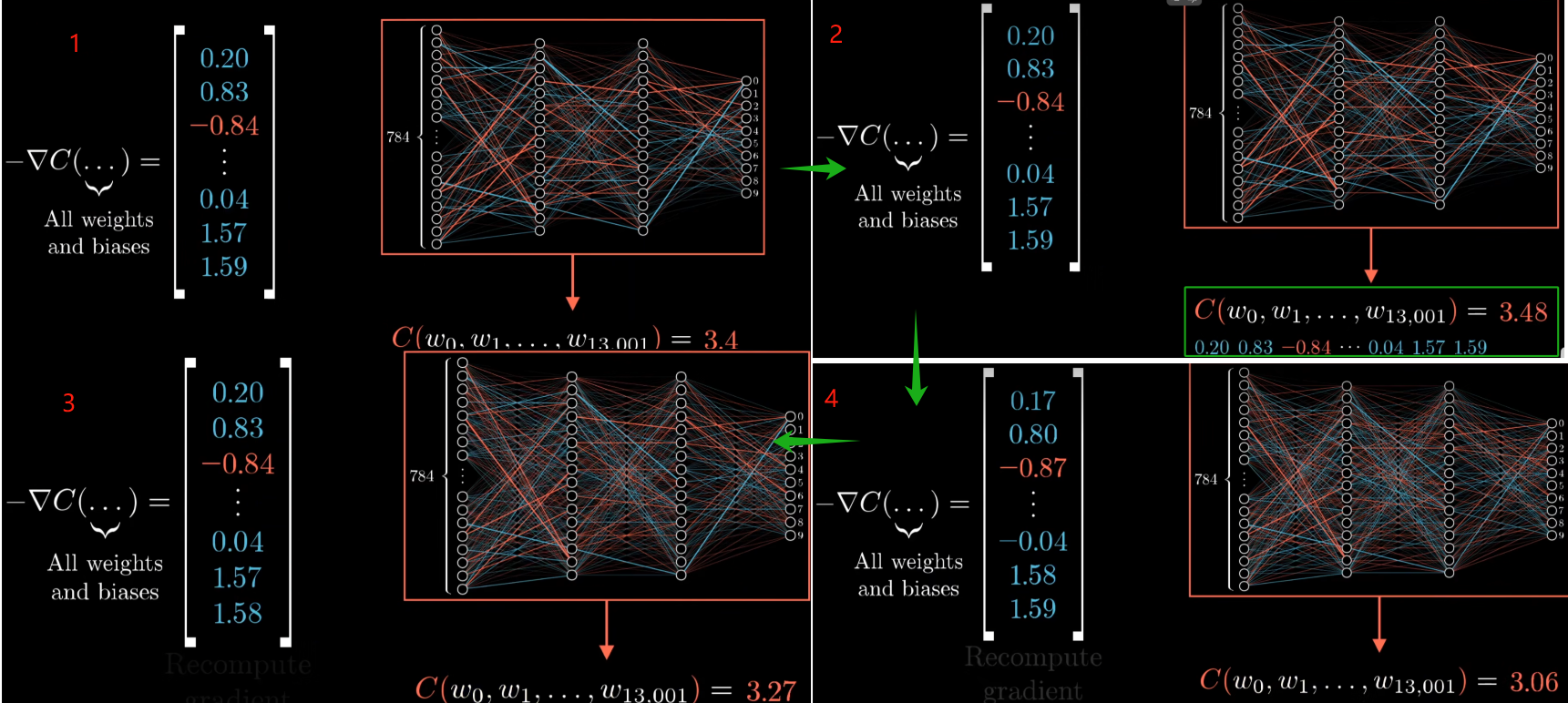
image-20240516221816669

✈深度学习之反向传播算法

  • 梯度向量的每一项大小是在告诉大家代价函数对于每个参数有多敏感

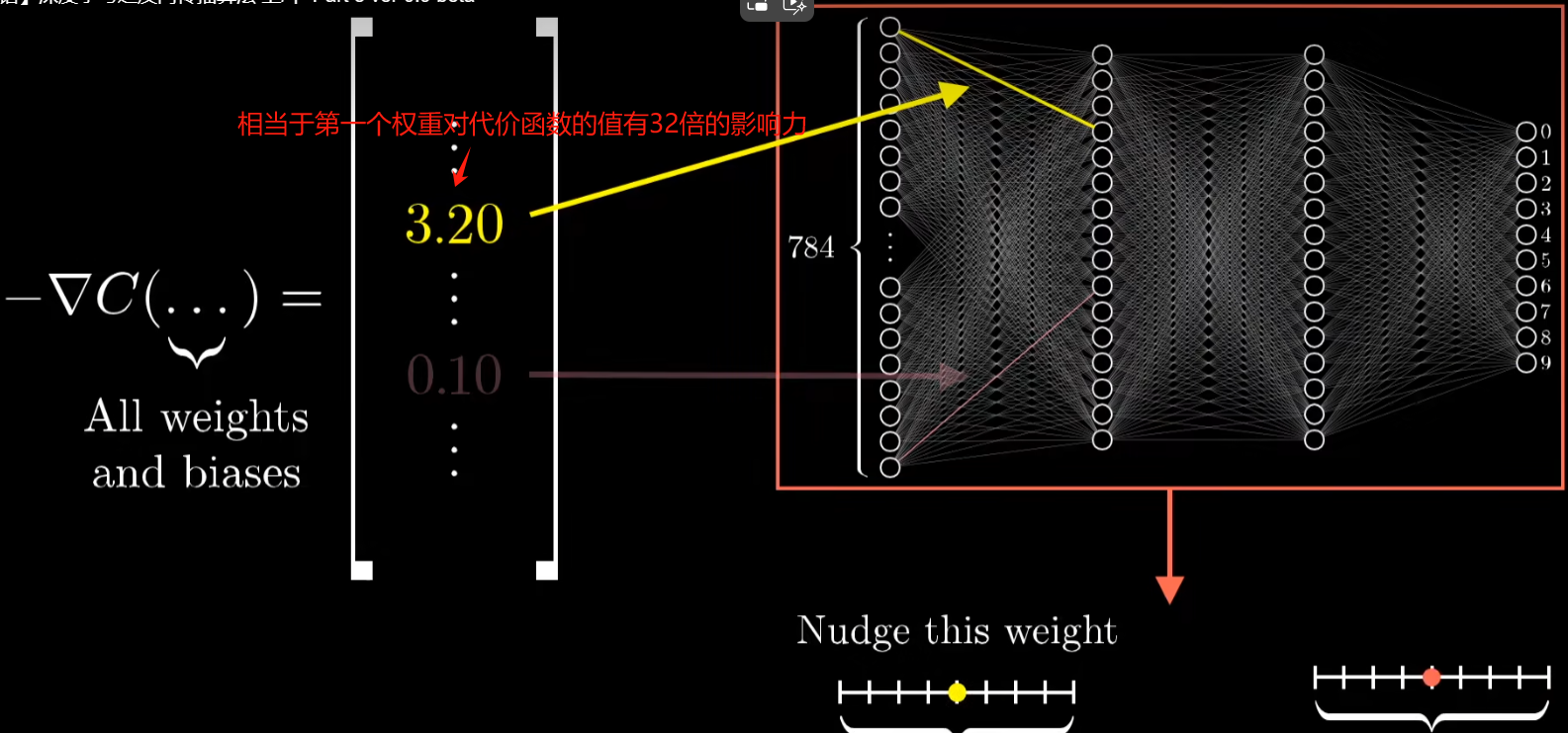
image-20240516222507331

  • 代价函数牵扯到对成千上万个训练样本的代价取平均值，

💥直观解释Transformer

  • 深度学习是机器学习的一种，机器学习采用数据驱动->反馈到模型参数，指导模型行为。

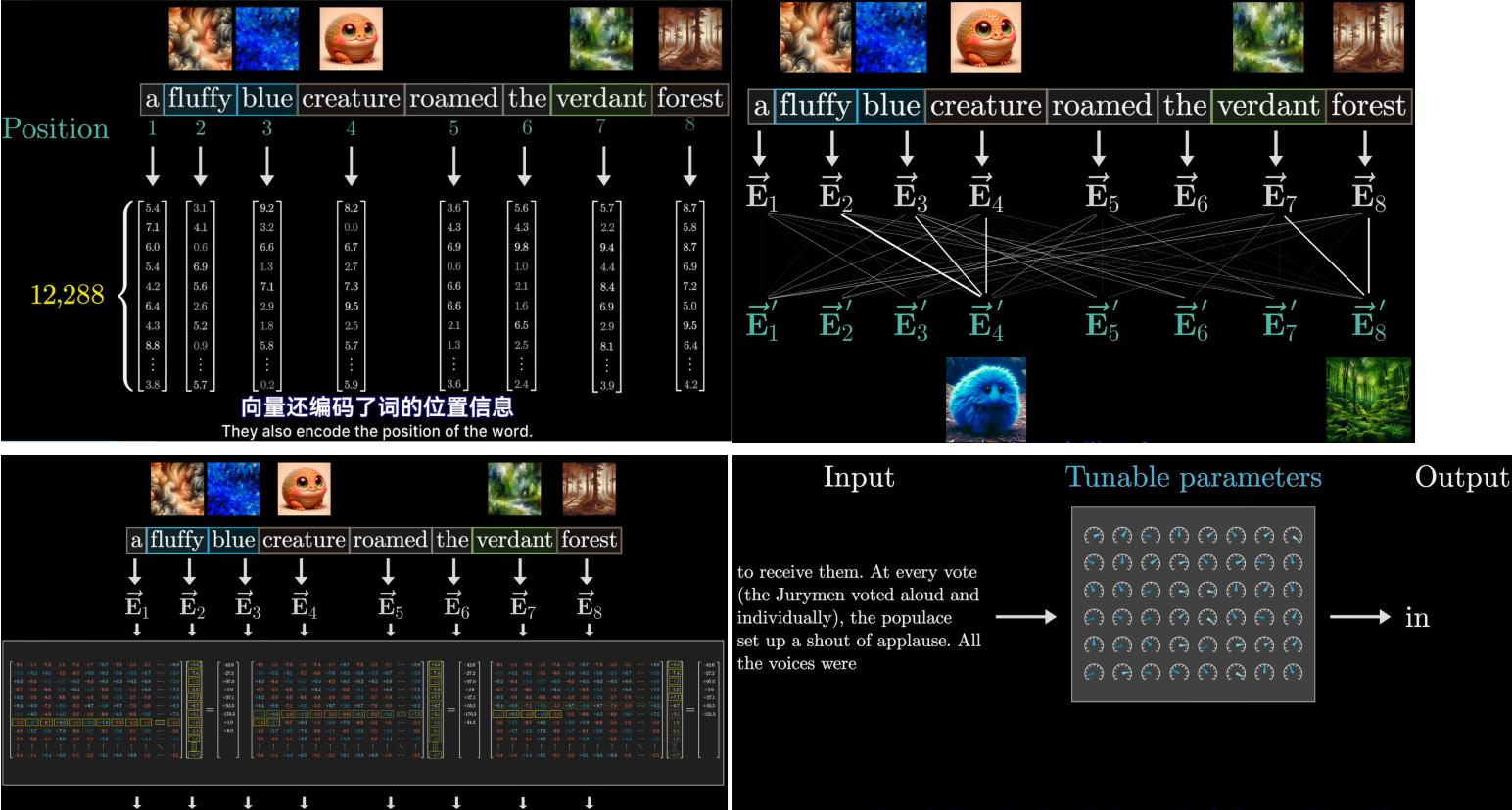
  • 机器学习的理念是不要试图在代码中明确定义如何执行一个任务，而是去构建一个具有可调参数的灵活架构

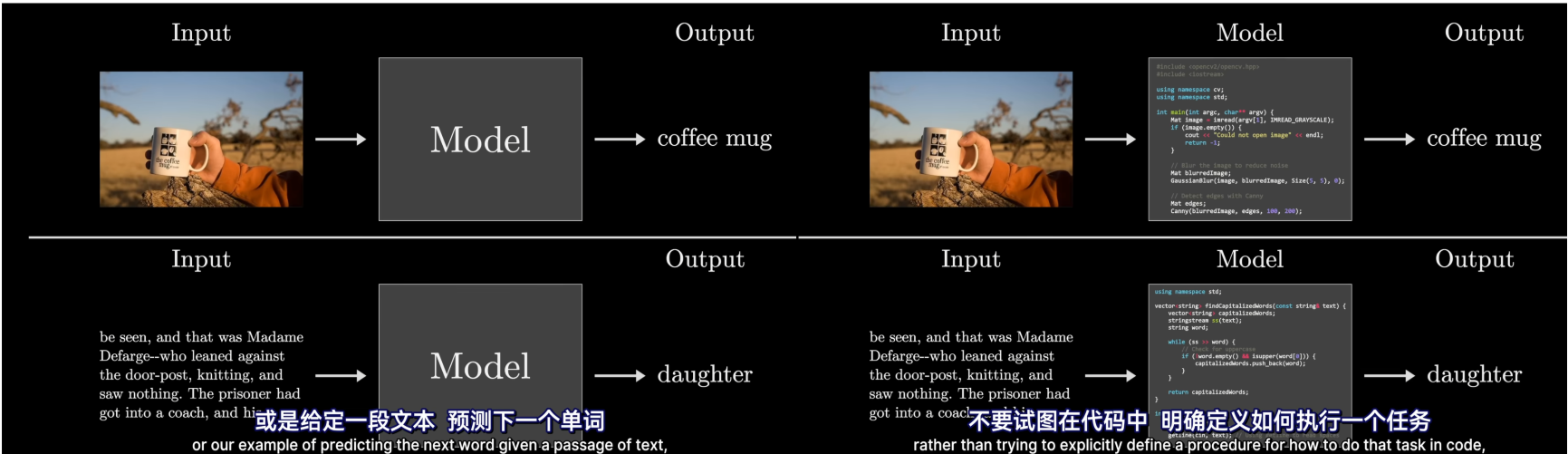
image-20240522154640459

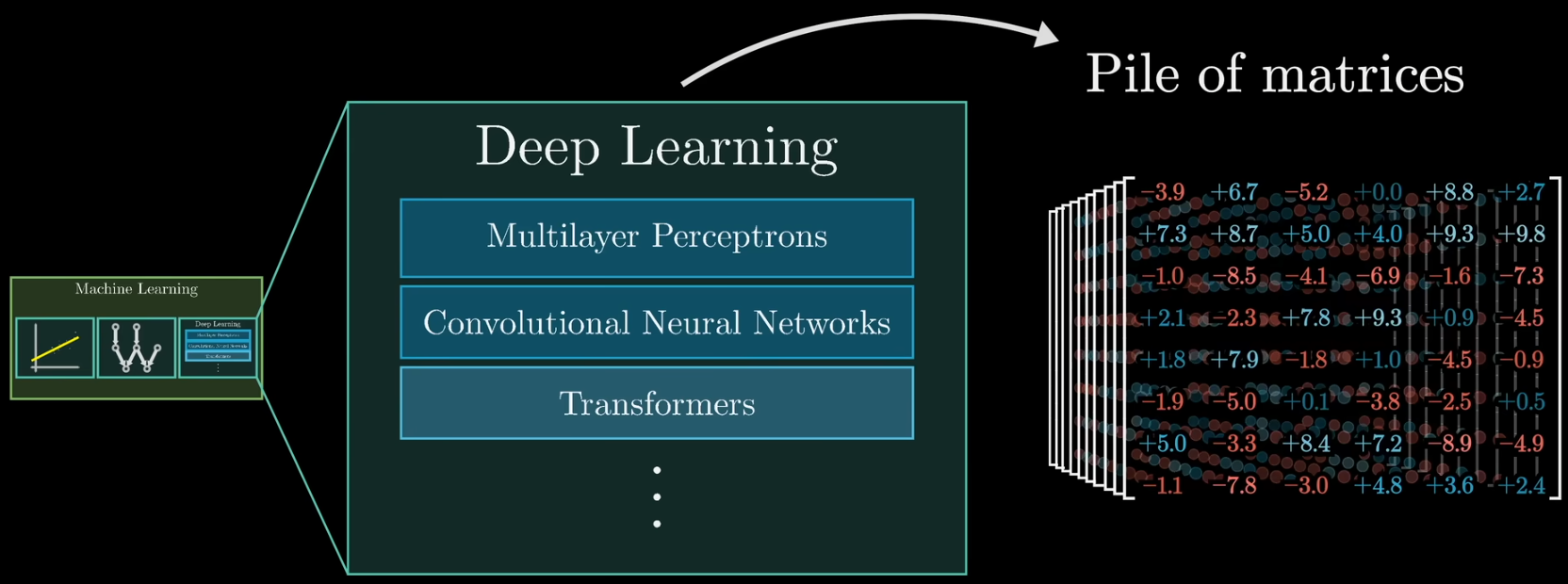
image-20240522155211600

image-20240522204209365

image-20240522205139273

image-20240522160147376

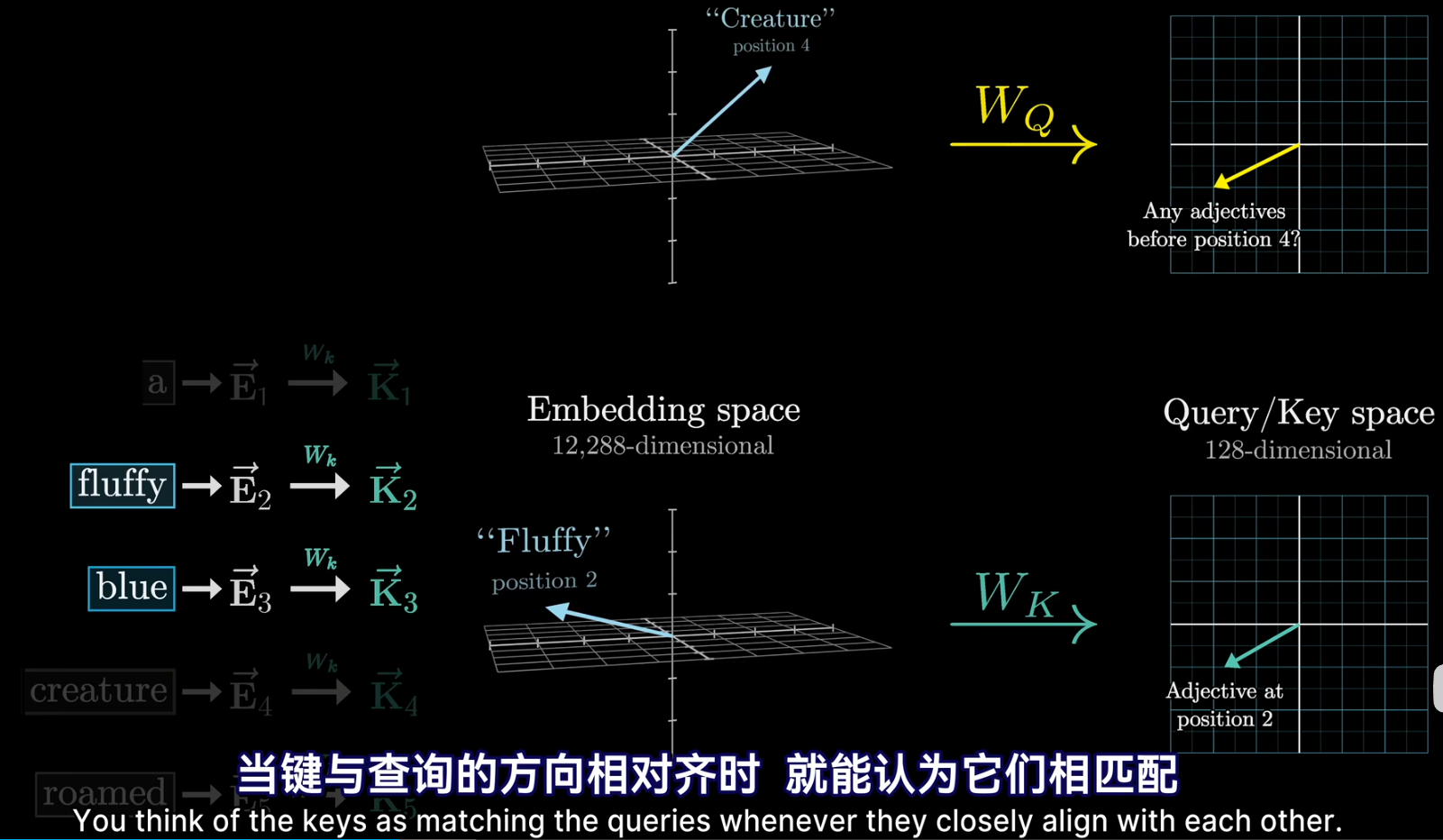
  • 两个向量的点积可以被看作是衡量他们对齐程度的一种方法；

image-20240522165201250

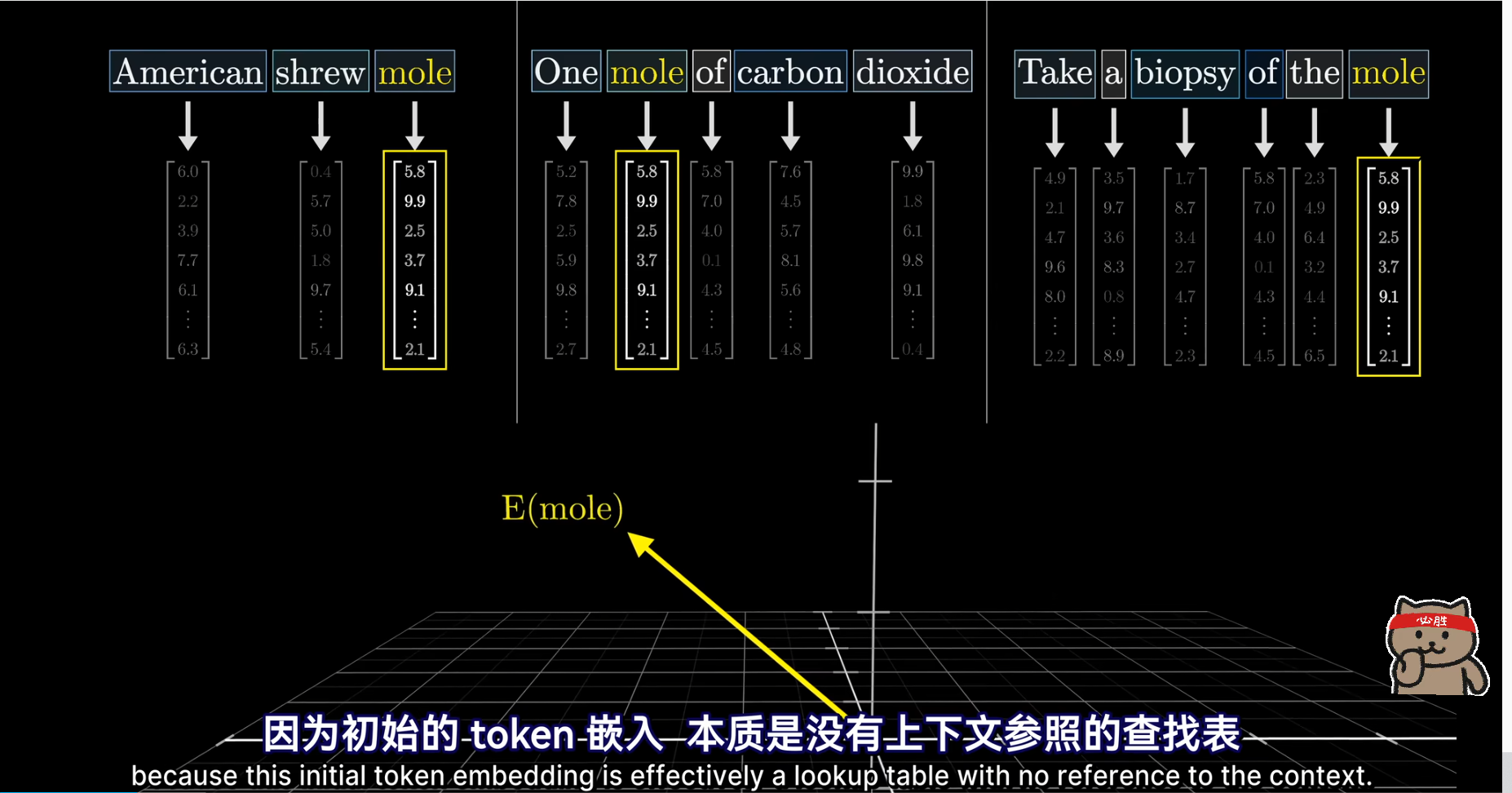
image-20240522205915319

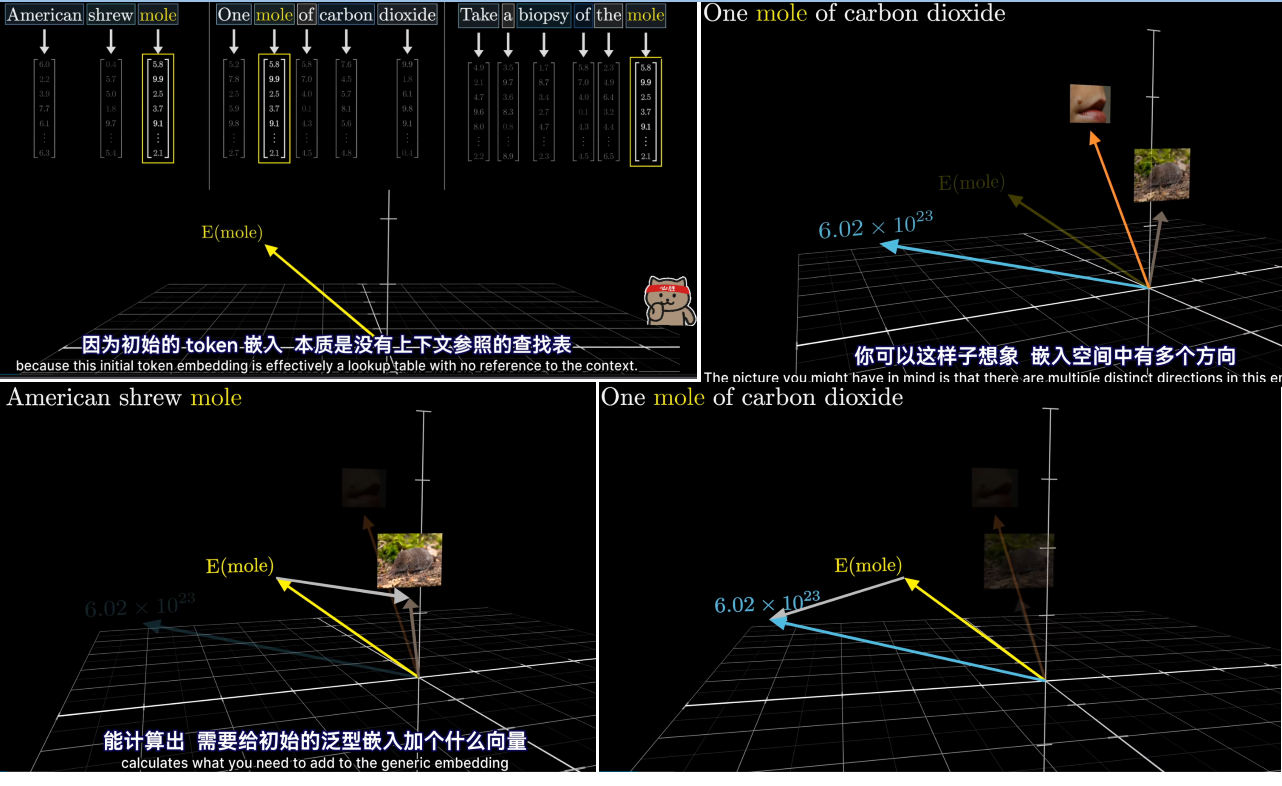
image-20240522211049908

要等到transformer这一步，周围的信息才能传递到该嵌入向量。可以这样想象，嵌入空间中有多个方向，编码了mole一词的不同含义，，而训练的好的注意力模块能计算出需要给初始的泛型嵌入加个什么向量才能把它移动到上下文对应的具体方向上

  • 这种网络一次只能处理特定数量的向量，称作它的上下文长度，上下文长度限制了Transformer在预测下一个词时，能结合的文本量 。预测下一个token的计算过程完全基于序列中的最后一个向量

image-20240522192413085

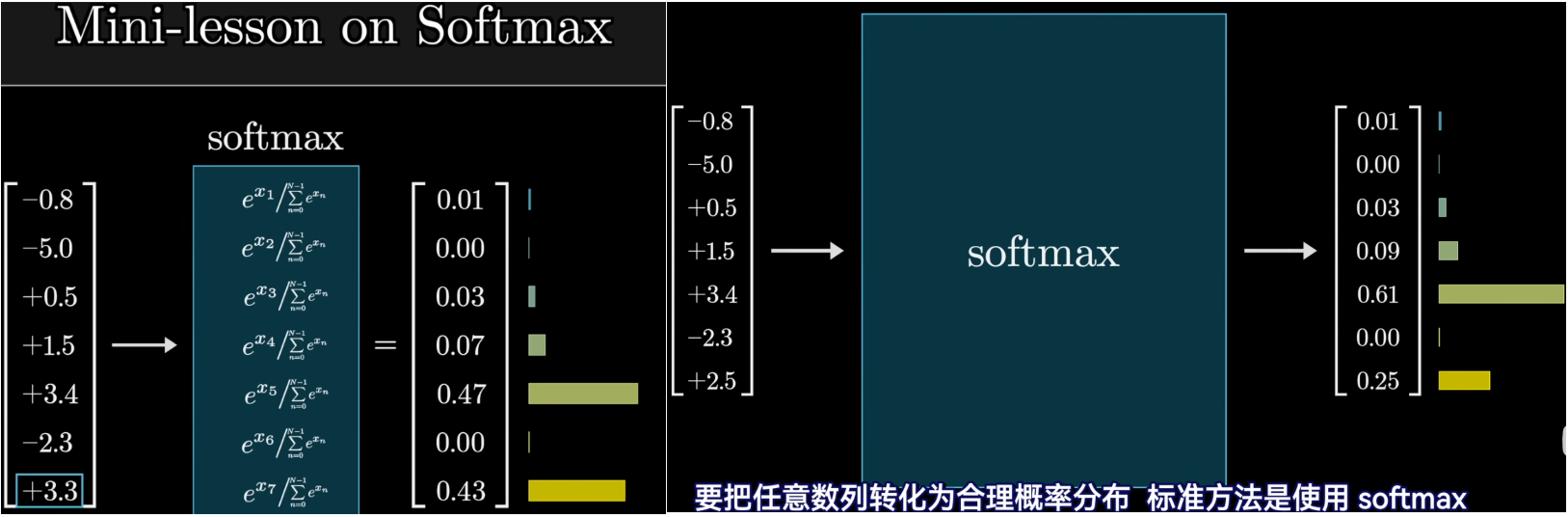
softmax函数

单头注意力机制

  • 每个词的初始嵌入是一个高维向量，只编码了该单词的含义和上下文没有联系（这么说不完全对，因为向量还编码了词的位置信息），用E表示这些嵌入式向量，最后的目标是通过一系列的计算产生一组新的更为精确的嵌入向量，比如那些经过形容词修饰的名词所对应的向量
  • 在深度学习中，模型的实际行为往往是很难解释的，因为他只是通过调整大量的参数来最小化某个代价函数

image-20240522214133017

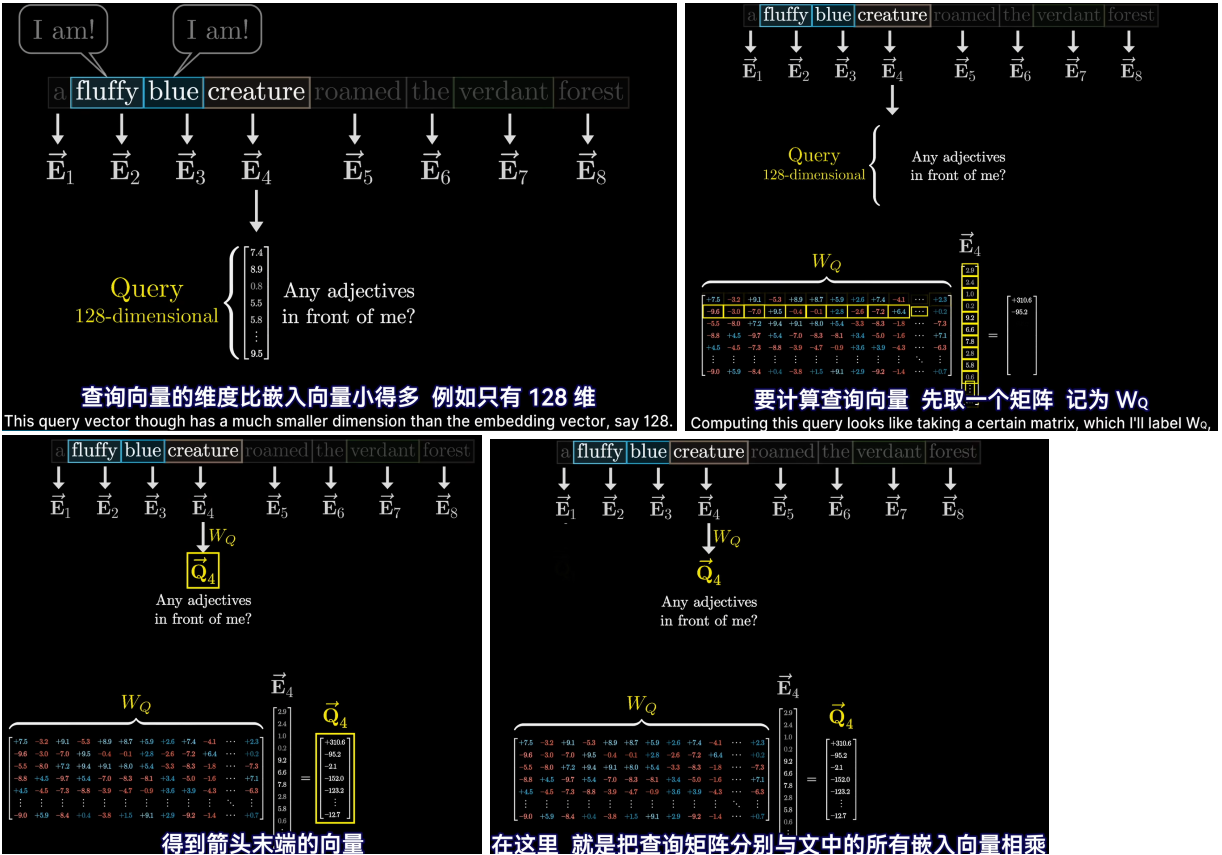
image-20240522221029201

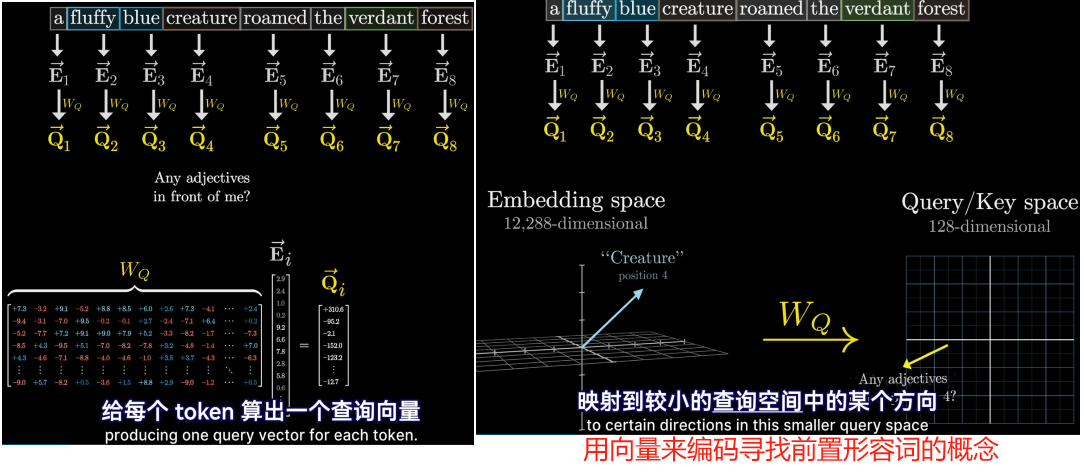
image-20240522221400791

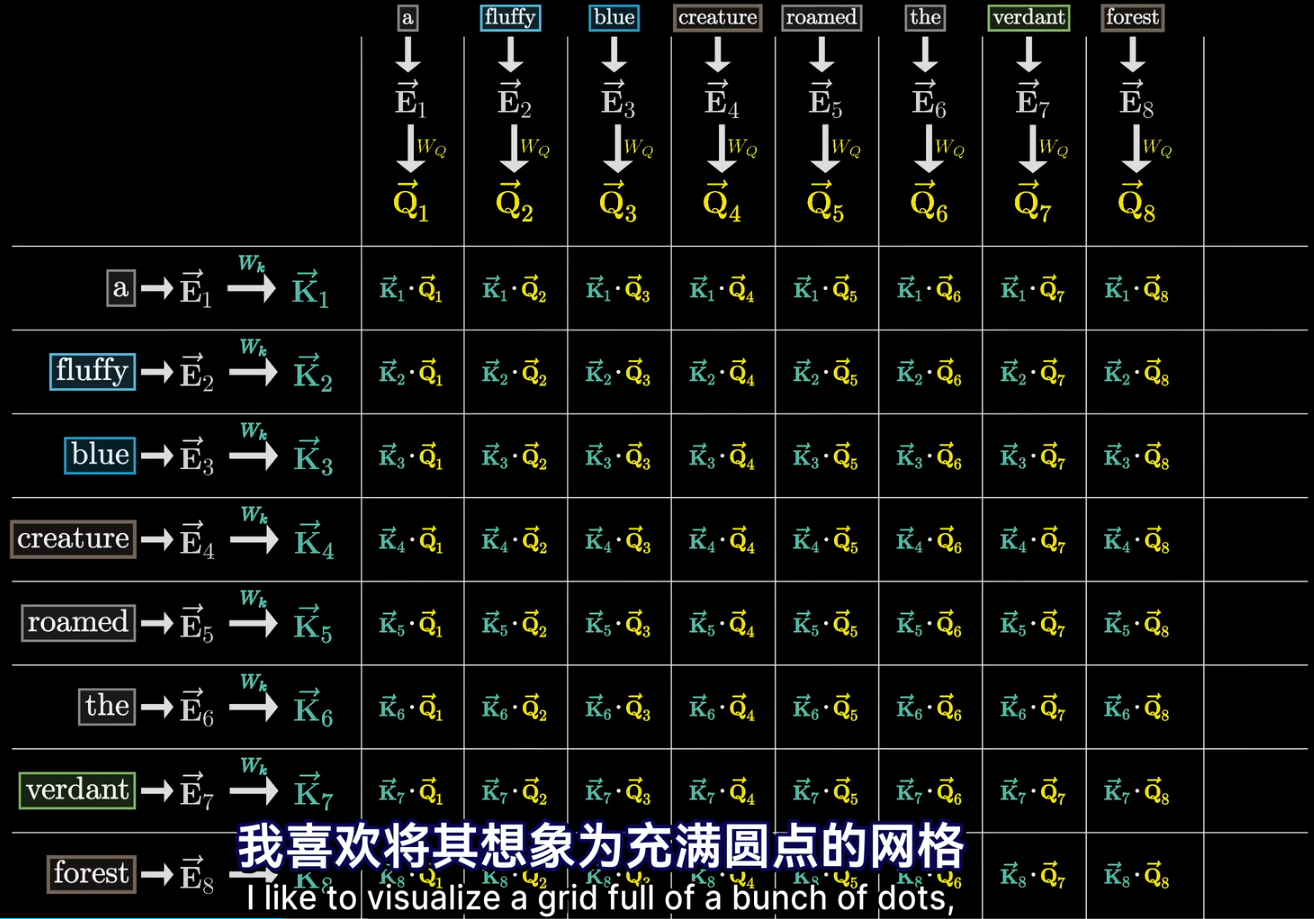
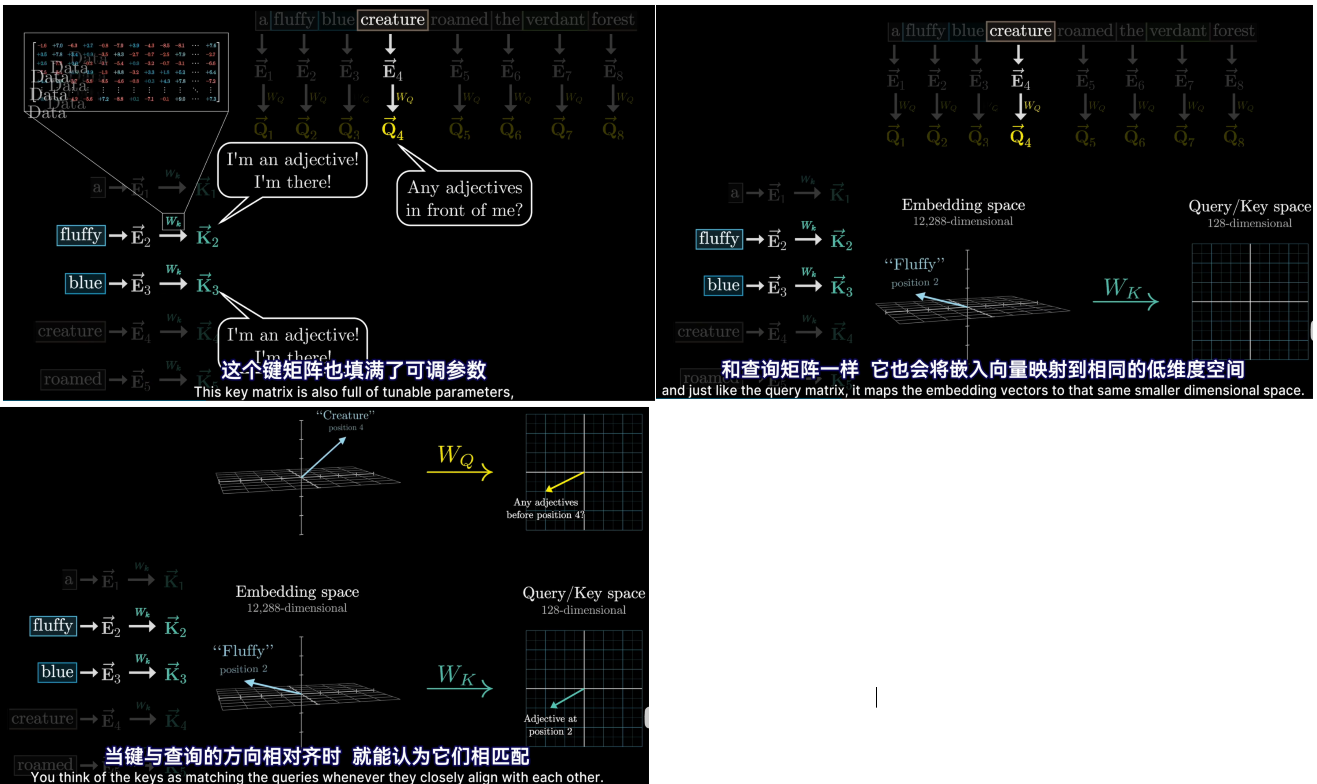
  • 同时还需要键矩阵，与每个嵌入向量相乘，产生第二个向量序列，称为键。从概念上讲可以把键视为想要回答的查询
  • 为了衡量每个键与每个查询的匹配程度，需要计算所有可能的键——查询对之间的点积

image-20240522221933995

image-20240522222050915

image-20240522222253166

image-20240522223422276