算法题总结
算法题
算法
动态规划
背包问题
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
常见的三种哈希结构
当我们想使用哈希法来解决问题的时候,我们一般会选择如下三种数据结构。
- 数组
- set (集合)
- map(映射)
这里数组就没啥可说的了,我们来看一下set。
在C++中,set 和 map 分别提供以下三种数据结构,其底层实现以及优劣如下表所示:
| 集合 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::set | 红黑树 | 有序 | 否 | 否 | O(log n) | O(log n) |
| std::multiset | 红黑树 | 有序 | 是 | 否 | O(logn) | O(logn) |
| std::unordered_set | 哈希表 | 无序 | 否 | 否 | O(1) | O(1) |
std::unordered_set底层实现为哈希表,std::set 和std::multiset 的底层实现是红黑树,红黑树是一种平衡二叉搜索树,所以key值是有序的,但key不可以修改,改动key值会导致整棵树的错乱,所以只能删除和增加。
| 映射 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::map | 红黑树 | key有序 | key不可重复 | key不可修改 | O(logn) | O(logn) |
| std::multimap | 红黑树 | key有序 | key可重复 | key不可修改 | O(log n) | O(log n) |
| std::unordered_map | 哈希表 | key无序 | key不可重复 | key不可修改 | O(1) | O(1) |
std::unordered_map 底层实现为哈希表,std::map 和std::multimap 的底层实现是红黑树。同理,std::map 和std::multimap 的key也是有序的(这个问题也经常作为面试题,考察对语言容器底层的理解)。
当我们要使用集合来解决哈希问题的时候,优先使用unordered_set,因为它的查询和增删效率是最优的,如果需要集合是有序的,那么就用set,如果要求不仅有序还要有重复数据的话,那么就用multiset。
那么再来看一下map ,在map 是一个key value 的数据结构,map中,对key是有限制,对value没有限制的,因为key的存储方式使用红黑树实现的。
其他语言例如:java里的HashMap ,TreeMap 都是一样的原理。可以灵活贯通。
虽然std::set、std::multiset 的底层实现是红黑树,不是哈希表,std::set、std::multiset 使用红黑树来索引和存储,不过给我们的使用方式,还是哈希法的使用方式,即key和value。所以使用这些数据结构来解决映射问题的方法,我们依然称之为哈希法。 map也是一样的道理。
这里在说一下,一些C++的经典书籍上 例如STL源码剖析,说到了hash_set hash_map,这个与unordered_set,unordered_map又有什么关系呢?
实际上功能都是一样一样的, 但是unordered_set在C++11的时候被引入标准库了,而hash_set并没有,所以建议还是使用unordered_set比较好,这就好比一个是官方认证的,hash_set,hash_map 是C++11标准之前民间高手自发造的轮子。
vector数组
vector容器求最值:用max_element()及min_element()函数,二者返回的都是迭代器或指针。
头文件
#include<algorithm>- 求最大值:
int maxValue = *max_element(v.begin(),v.end()); - 求最小值:
int minValue = *min_element(v.begin(),v.end());
- 求最大值:
vector容器求总和:
头文件
#include <numeric>int sum = accumulate(v.begin(), v.end(), 0);
滑动窗口
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
在暴力解法中,是一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环完成了一个不断搜索区间的过程。
所以只用一个for循环,那么这个循环的索引,一定是表示 滑动窗口的终止位置。
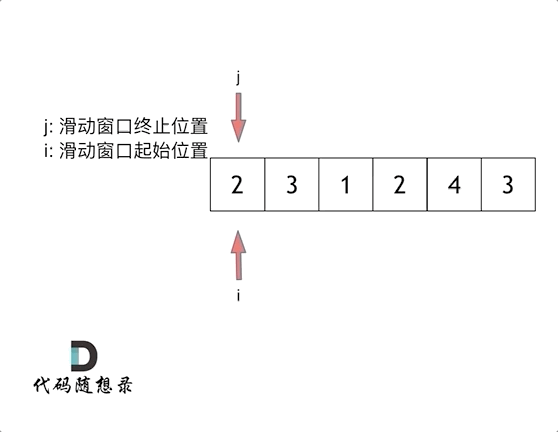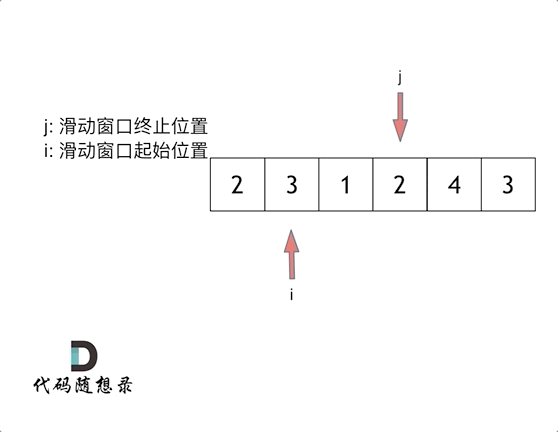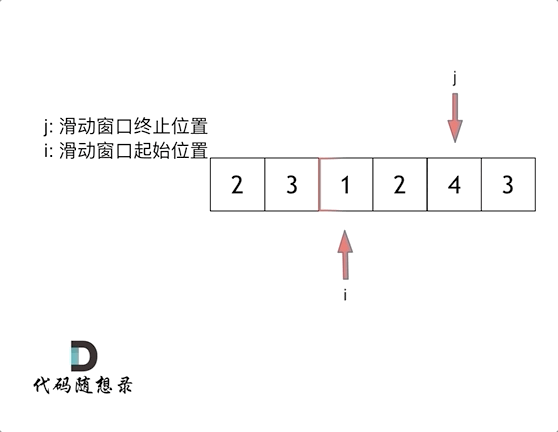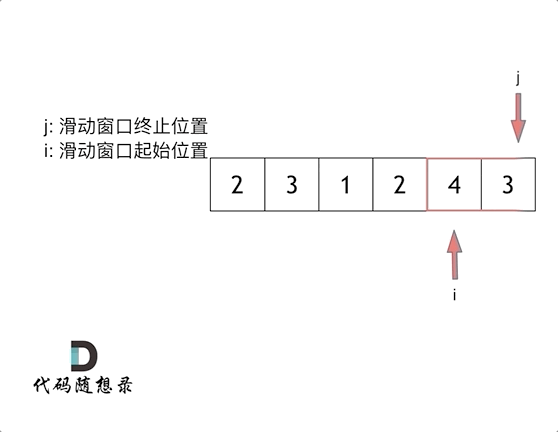
实现滑动窗口,主要确定如下三点:
窗口内是什么?
如何移动窗口的起始位置?
如何移动窗口的结束位置?
```c++
class Solution {
public:
int minSubArrayLen(int s, vector& nums) {
int result = INT32_MAX;
int sum = 0; // 滑动窗口数值之和
int i = 0; // 滑动窗口起始位置
int subLength = 0; // 滑动窗口的长度
for (int j = 0; j < nums.size(); j++) {
sum += nums[j];
// 注意这里使用while,每次更新 i(起始位置),并不断比较子序列是否符合条件
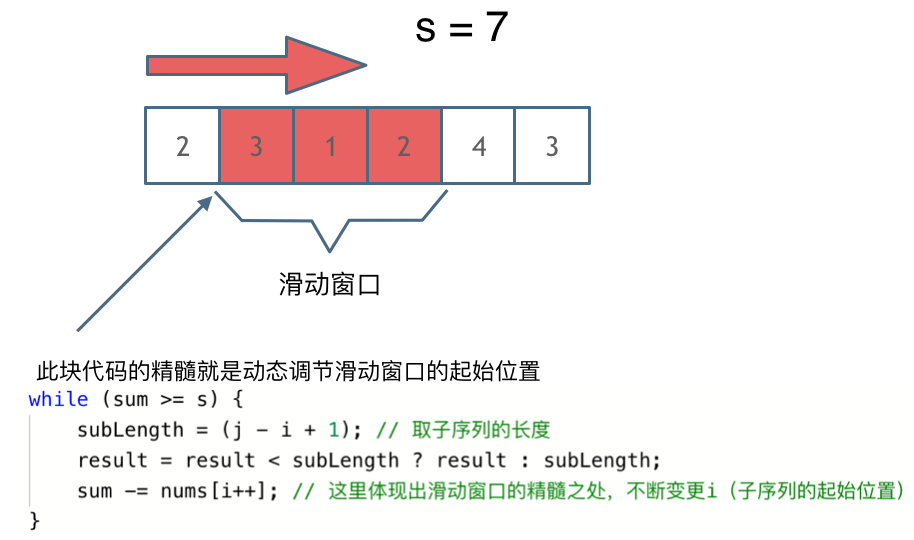
while (sum >= s) {
subLength = (j - i + 1); // 取子序列的长度
result = result < subLength ? result : subLength;
sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处,不断变更i(子序列的起始位置)
}
}
// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
return result == INT32_MAX ? 0 : result;
}
};
-
- 
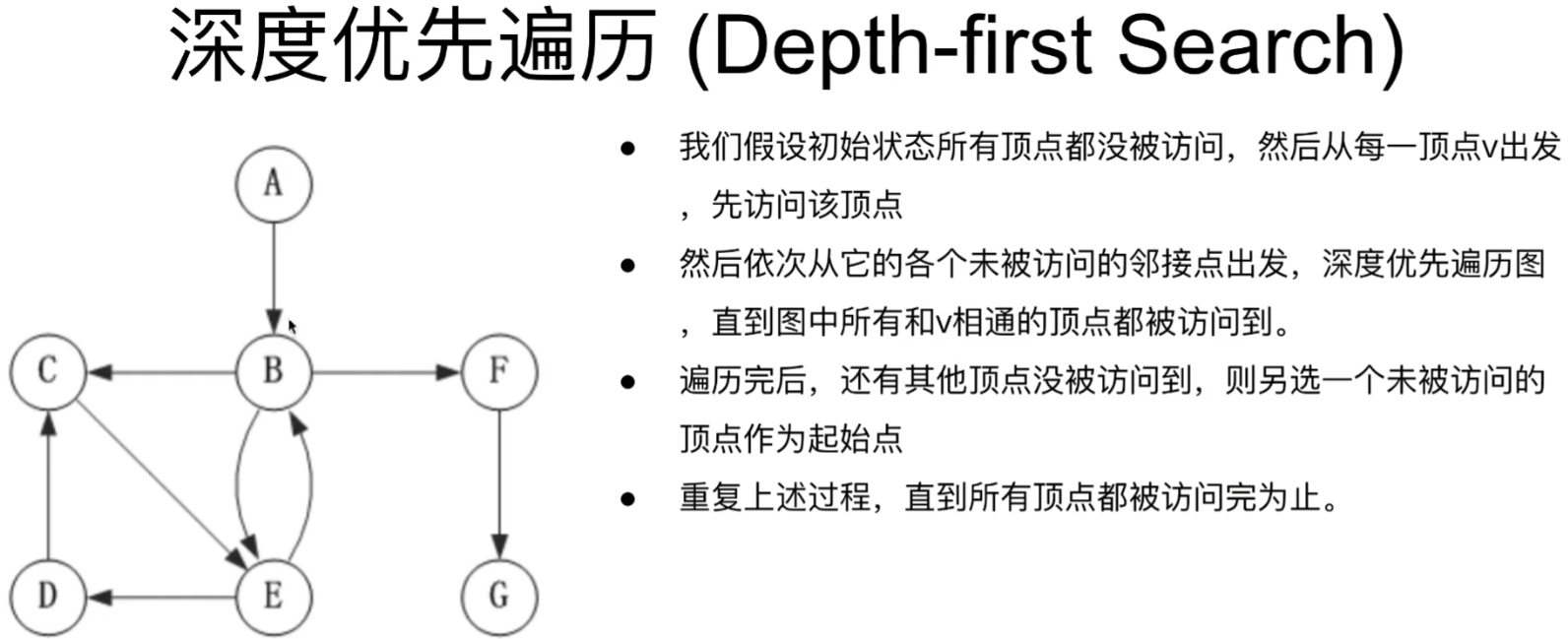
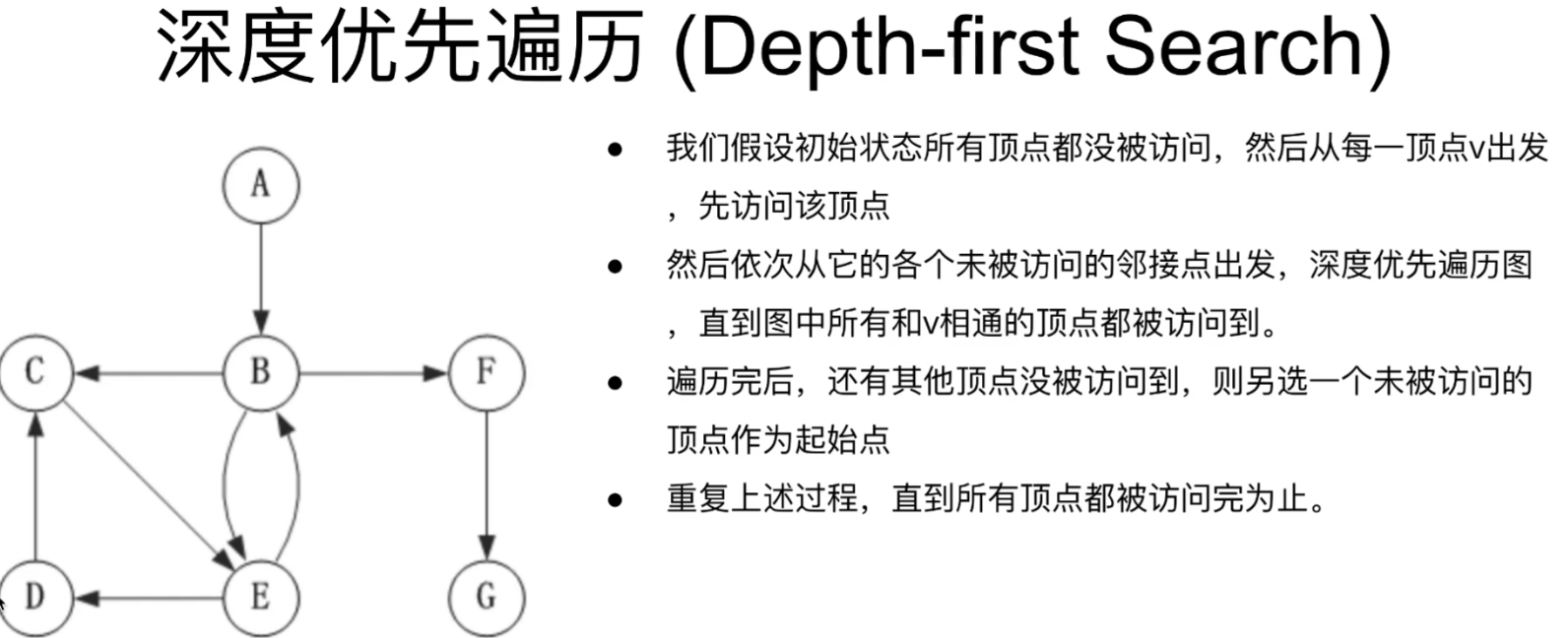
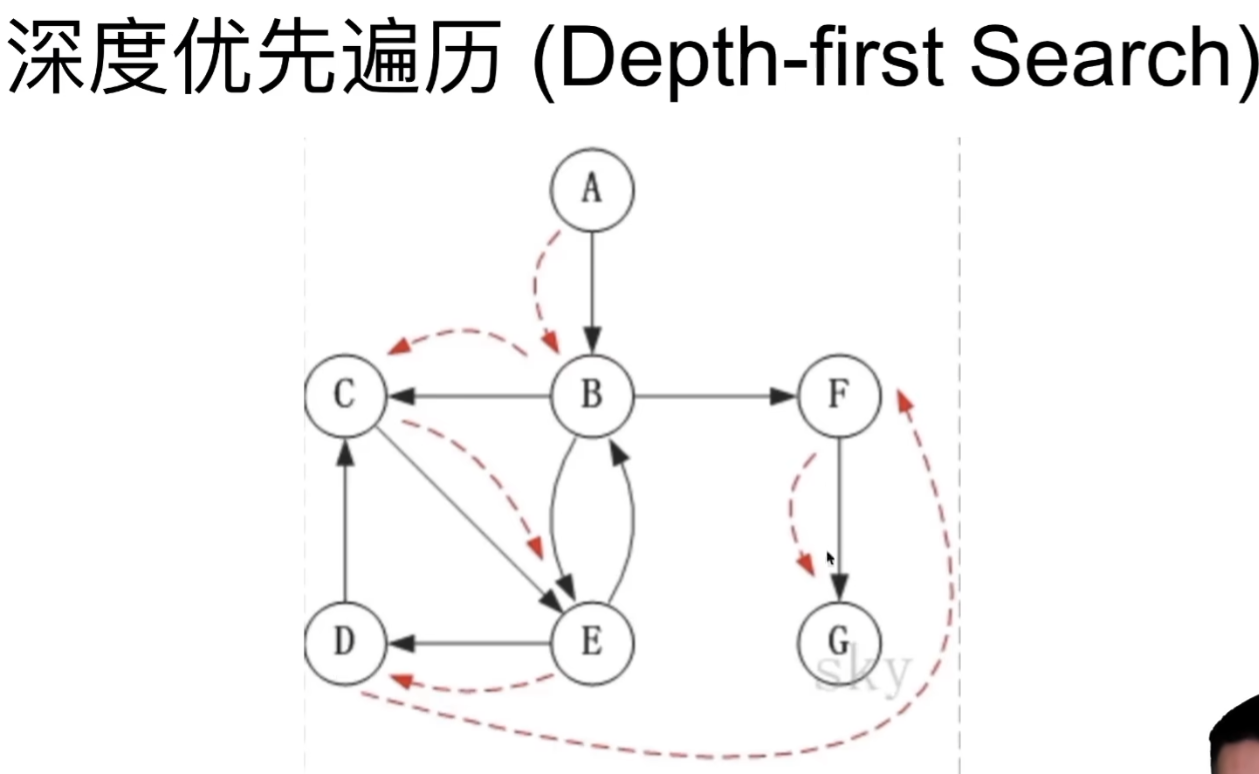
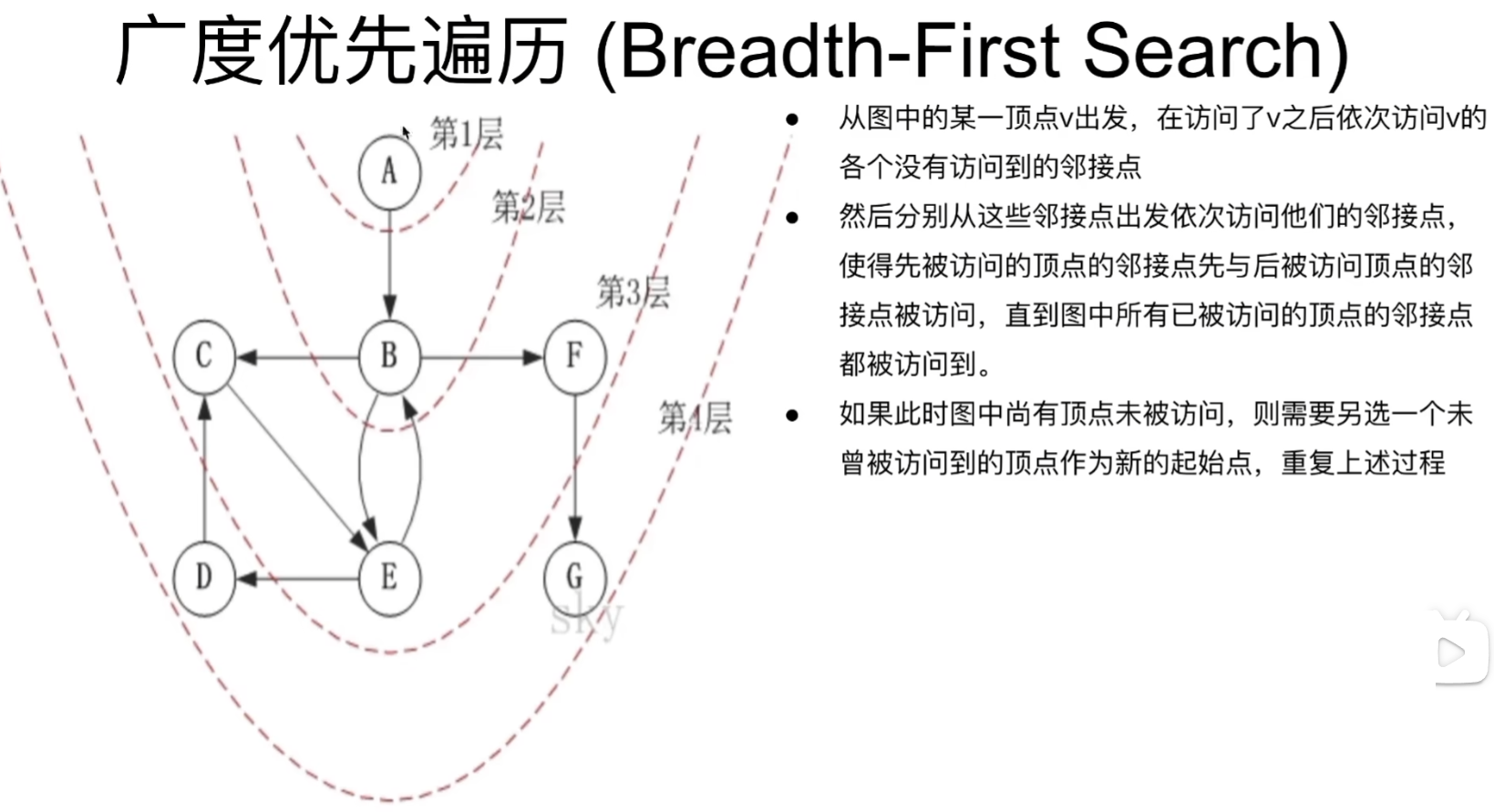
### 图的BFS和DFS
## 周赛
## 双周赛129
[100292. 找出所有稳定的二进制数组 I](https://leetcode.cn/problems/find-all-possible-stable-binary-arrays-i/)
给你 3 个正整数 `zero` ,`one` 和 `limit` 。
一个二进制数组`arr` 如果满足以下条件,那么我们称它是 **稳定的** :
- 0 在 `arr` 中出现次数 **恰好** 为 `zero` 。
- 1 在 `arr` 中出现次数 **恰好** 为 `one` 。
- `arr`中每个长度超过`limit`的子数组都同时包含 0 和 1。
请你返回 **稳定** 二进制数组的总数目。
由于答案可能很大,将它对 `109 + 7` **取余** 后返回。
```c++
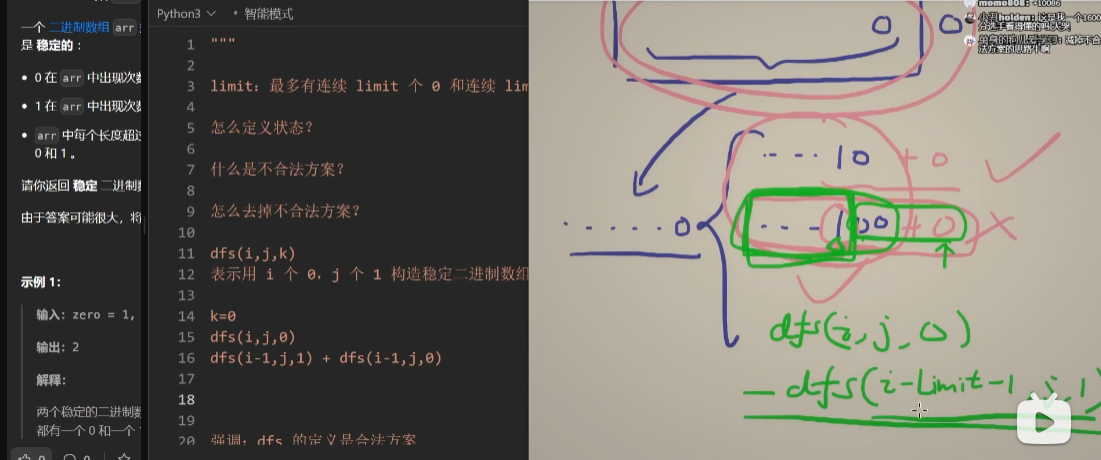
/*limit:最多有连续的limit个0和连续个limit个1
dp(i,j,k)表示用i个0,j个1构造的稳定二进制数组的方案数,其中第i+j个位置要填k
k=0
dp(i,j,0)=dp(i-1,j,1)+dp(i-1,j,0)-dp(i-limit-1,j,1)
*/
class Solution {
public:
typedef unsigned long long int Ln;
const Ln mod = 1e9 + 7;
int numberOfStableArrays(int zero, int one, int limit) {
vector<vector<vector<Ln>>> dp(zero + 1, vector<vector<Ln>>(one + 1, vector<Ln>(2, 0)));
for(int i = 1; i <= limit; i++) {
if(i <= zero) dp[i][0][0] = 1;
if(i <= one) dp[0][i][1] = 1;
}
for(int i = 1; i <= zero; i++) {
for(int j = 1; j <= one; j++) {
if(i-limit > 0) dp[i][j][0] = ((dp[i-1][j][1] + dp[i-1][j][0]) + mod - dp[i-limit-1][j][1]) % mod;
else dp[i][j][0] = (dp[i-1][j][1] + dp[i-1][j][0]) % mod;
if(j-limit > 0) dp[i][j][1] = ((dp[i][j-1][0] + dp[i][j-1][1]) + mod - dp[i][j-limit-1][0]) % mod;
else dp[i][j][1] = (dp[i][j-1][0] + dp[i][j-1][1]) % mod;
}
}
return (dp[zero][one][0] + dp[zero][one][1]) % mod;
}
};
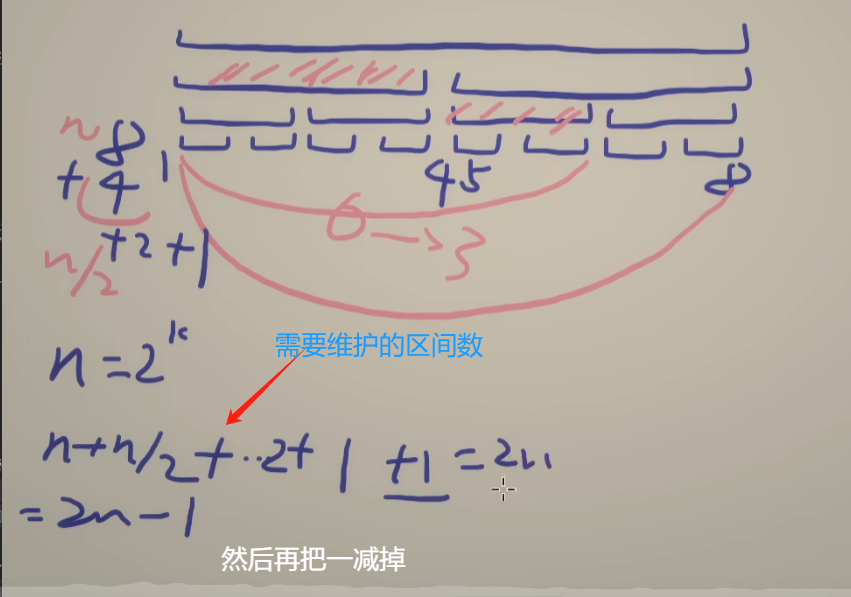
线段树
lambda 函数
模拟真题
23科大讯飞提前批
2024.05.23
小红的字符串切割
题目描述
小红拿到了一个字符串,她希望你帮她切割成若干子串,满足以下两个条件:
- 子串长度均为不小于 3 的奇数。
- 子串内部的字符全部相同。
输入描述
第一行输入一个正整数n,代表字符串长度。第二行输入一个字符串,仅由小写字母组成。
输出描述
如果无解,请输出-1。否则按顺序输出若干个字符串,用空格隔开。
输入示例
11 |
输出示例
aaa bbb bbbbb |
提示信息
在样例中,长度为 8 的 bbb..b 子串在样例输出中被分为了 bbb 和 bbbbb,在只要满足题目给定的条件下,将其分为 bbbbb 和 bbb 也对。 |
/* |