基于投影变换的锥束层析成像重建方法
A reconstruction method for cone-beam computed laminography based on projection transformation
基于投影变换的锥束层析成像重建方法
要解决的问题
- 现有的解析CL重建方法大多忽略了CL扫描结构下的投影数据不严格满足标准滤过反投影( FBP )或费尔德坎普- Davis - Kress ( FDK )方法条件的问题。
解决方案
- 由于直接对原始CL数据进行滤波,**没有考虑CL旋转轴倾斜角度的影响,这会影响重建图像的质量 **。
- 针对这种情况,提出了一种基于投影变换的锥束CL数据转换方法,也称为CL重投影( CLRP )。可以对采集的CL投影进行校正,使其满足滤波要求。
技术路线
- 建立了一个虚拟的CT探测器,并利用CLRP将已知的CL数据转换为在虚拟探测器上的投影,该方法**主要实现将锥束CL数据转换为符合FDK要求的数据,然后,采用锥束CT中常用的FDK方法对转换后的数据进行重建。**FDK方法的滤波器不需要人为优化,可以使用已有的合适的滤波器。通过以上两个步骤实现CL重构。
- 本文的**难点**在于如何准确地将CL数据转换为CT数据,以及转换后如何获取用于CT重建的扫描参数。我们解决了设计等效转换手段的问题,该转换手段被称为CL重投影( CLRP )算法。与现有的CL - FBP重建方法相比,CLRP方法不仅可以使变换后的数据严格满足普通FBP或FDK的要求,而且可以实现现有CT算法在CL重建中的应用。
结果
- 计算机仿真和实验结果表明,CLRP算法能够准确地将原始CL数据转换为满足FDK方法的CL数据。CLRP可以在一定程度上减少信息混叠。与现有的CL - FBP算法相比,采用CLRP - FDK方法进行CL重建可以有效地减少图像伪影。
1.introduction
Lauritsch等人基于相应的调制传递函数,他们提出了一种通用的四步滤波器设计概念,用于对投影图像进行滤波。重建切片图像的平面空间分辨率较高,但深度分辨率相对较差,这是由于层析成像扫描中采样不完全造成的。他们分析了平行束下的采样和应用,但**没有进一步讨论扇形束和锥形束的几何结构。**
本课题组在前期研究[ 12 ]中提出了适用于弧形轨道锥束CL扫描模式的FBP重建算法(称为CL - FBP)。直接执行传统的S - L过滤器来过滤原始CL数据。利用修正后的反投影计算公式进行重建。
Myagotin等人解决了平行束几何条件下CL体积重建的不适定问题,并基于FBP方法提出了一种计算高效的重建方法[ 17 ]。
——总结
这些方法都忽略了一个问题,即在CL扫描结构中,上面提到的连接线并不垂直于旋转轴,因此CL扫描系统中的投影数据并不严格符合FBP算法。虽然它们的执行效率很高,但是这个问题会导致重建图像中出现伪影。
Zhao等人结合边缘信息扩散过程提出了一种用于平面物体检测的CL重建方法[ 25 ]。通过这种方法,可以有效地抑制CL扫描数据不完整引起的层间混叠和模糊。**但如何加速它们成为一个亟待解决的问题。**
2.推导CL扫描数据的转换方法
前提:
假设所有的投影数据都是经过校正的,即点源产生的X射线在传播过程中的强度被认为是一个常数。在理想条件下进行X射线投影时,适当改变探测器的姿态对投影结果没有本质的影响。
3.提出CL重构参数的转换方法
知识点
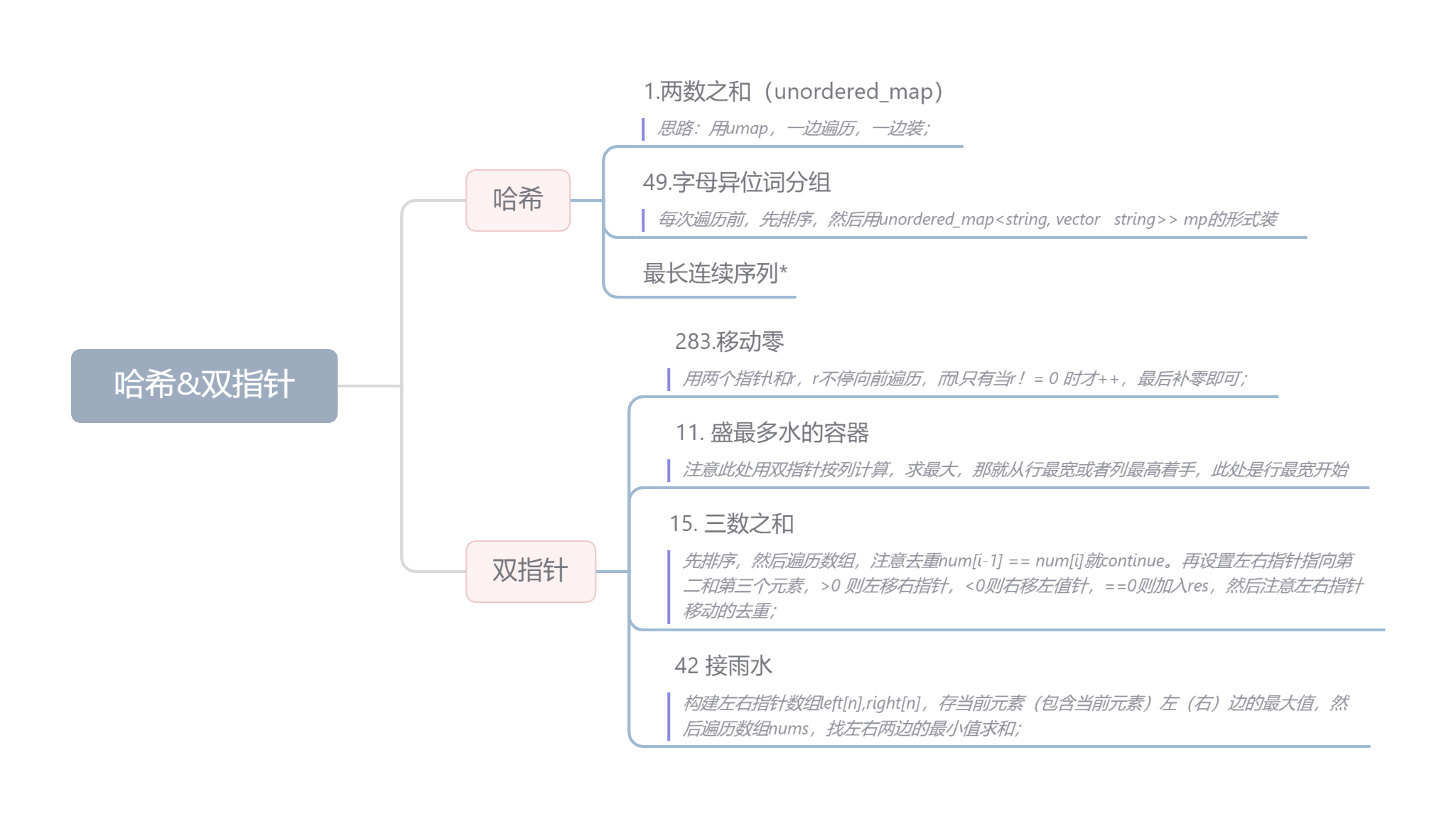
重建算法
解析法(数学基础为Radon变换)——存在伪影
对于平行束或扇束CT,应用最广泛的解析算法是滤波背投影( FBP )。
对于锥束几何,最常用的方法是费尔德坎普- Davis - Kress ( FDK )
标准的FBP或FDK算法需要满足**旋转台中心点与射线源焦点之间的连线穿过探测器中心点。这个连线也应该垂直于探测器平面和旋转轴**。
迭代法(数学基础是求解方程组)——效率较低
——与解析重建算法相比,迭代重建算法具有较强的通用性和较好的重建质量[ 18-20 ]。无论扫描轨 迹多么复杂,投影数据都可以通过迭代的方式进行重建[ 21-24 ]。
- 代数重建技术ART
- 基于全变分的ASDPOCS(虽然重建速度较慢,但当图像噪声影响较大或投影数量较少时,ASD - POCS方法明显优于其他算法。)
- 基于Krylov子空间的共轭梯度最小二乘算法[ 23 ]和基于统计的最大似然估计方法[ 24 ]